前言：
此贴为 【新增茶杯犬】5只防水宠【含蓝晶龙】防御概率及稳定性测评【测472次】 的后续补充改进篇，详细阐述稳定性分析方法！ 稳定性评价以本文为准！（由于受时间所限，前文的分析方法较为粗糙，不够全面客观。本文更科学客观）
此贴可视为一篇微型论文，公式的适用性验证、各项数据的繁琐计算及图表的制作都花了极长时间；
此贴最后的附件为每只宠物的472次测试的原始数据扫描件，如有兴趣做研究的朋友可以下载。
稳定性分析：
稳定性概念：
波动越剧烈，稳定性越差；波动越平稳，稳定性越好。 有的人会讲：我感觉某某宠物经常出现多少多少连防，（或者说连防挺多的，）稳定性怎么会这么差？ 我在此说明： 多少连防，它跟“稳定性”不是一个概念， 不论是“连防”还是“多少连防”，那都是玩家对“期望中的事或物”的感官判断，有失客观，谁都希望自己的宠物能出现多少多少连防，所以往往会忽略它不防御又有多少？
分析前提：
各个宠物都具有其防御特性，而不是完全随机的。 如是完全随机的，则此文没有意义！本人一星期的劳动成果泡汤o(╯□╰)o
分析思路：
本人将每个宠物的测试数据当做这个宠物的防御性能“样本”，因为每个宠物的防御或是不防御在它的生命中是无限多的，我所测的只能说是“总体”中的“样本”，这个“样本”的量越大，依靠它分析所获得的结论越准确。所以每个宠物我都测了472次，来保证数据的准确性。样本中只存在2个值，分别为“防御”和“不防御”，根据宠物的防御概率在40%左右可以得知：样本中“不防御”的数量肯定多于“防御”的数量。 那么我如果要分析宠物防御性能的稳定性，是否应该选取其中更多数量的“不防御”来作为分析的原始数据呢？答案是肯定的，原因有俩：1、样本中只有2个值，其中任意一个值的稳定性都能反映出另外一个值的稳定性，即防御越稳定，不防御也越稳定，反之亦然；2、选取量多的那个值来分析，得到的结论更准确。
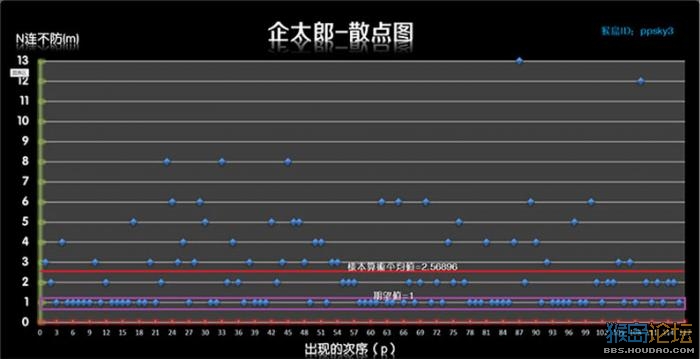
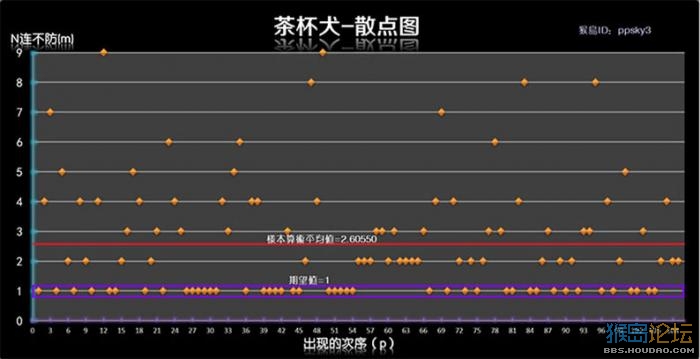
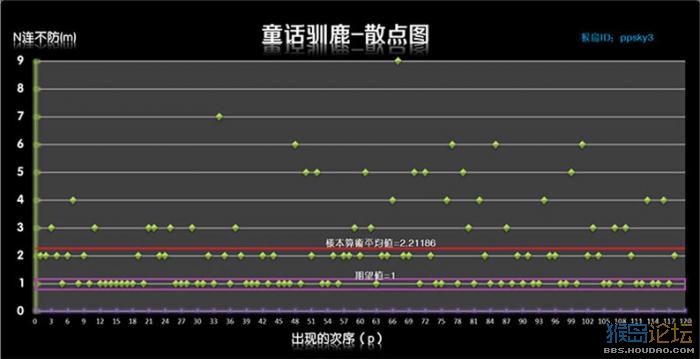
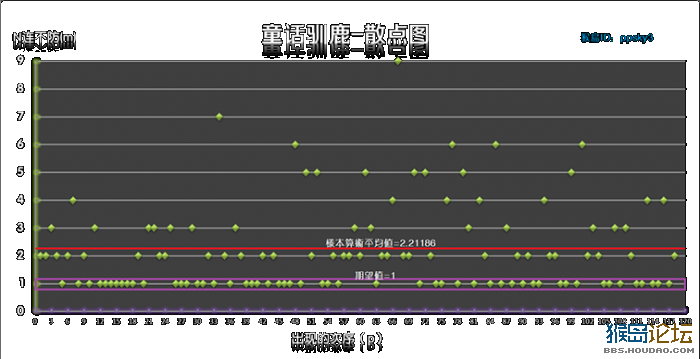
所以第一步确定了，那就是以样本中的“不防御”为原始数据来分析稳定性。 我把所有的“不防御”做为“一个个小团体”统计起来，把这“一个个小团体”命名为“N连不防”（简称“N不防”），把它们做成图表的形式直观的展示出来。称之为“某某宠物-散点图”，5个宠物的散点图见下方（点击放大查看）：
分析方法：
以上散点图中，X轴为“出现的次序”，就是时间轴；Y轴为“N连不防”，为数据轴。 （例如：在“企太郎”这张图表中，当p=60时，m=1；当p=33时，m=8。 它们代表的意思分别为： 在N不防样本中，第60个N不防为1不防； 第33个N不防为 连续8次不防御，即8不防。 从图中可以看出，企太郎的测试数据中，出现的最高数值为13不防。
通过上面这段话，大家应该能看懂这个图表了。 我的分析方法便是：分别从Y轴方向和X轴方向这两方面来判定宠物防御的稳定性， Y轴方向为N不防的数据分布情况，X轴方向则是N不防在时间上的分布情况。 （Y轴） 数据分布的波动越稳定，则宠物防御越稳定； （X轴）N不防出现的时间（次序）分布越均匀，则宠物防御越稳定。
Y轴方向： 我参考统计学中的样本标准差来分析， 样本标准差反映的是一组抽样数据相对它们的算术平均值的离散程度，离散程度越大，即样本标准差越大，则该组数据的波动越大，稳定性越差。
样本标准差公式：
说到这里，肯定几乎所有人都认为我会立即开始着手代入数据计算了是吧？如果你是例外，那我可以肯定的说你是世界上第二个聪明的人！因为你发现了问题。问题在哪里？问题就在于样本标准差公式的本质意义，大家都理解了吗？ 样本标准差公式的本质意义是：以样本算术平均值为参照物，来计算数据的离散程度，这个离散程度是相对于算术平均值的，这个算术平均值是发明这个公式的人的“期望值”，他或她期望相对于算术平均值的离散程度越低越好。 那我们呢？我们大家的期望值是什么？ 我们的期望无疑是“最好不要出现连续的不防御啊”，在图表中的体现就是：我们的期望值=1 。 所以我们应当计算 样本相对于【1】的离散度， 对于【1】的离散度越小，则越稳定！
在此，我将上述 样本标准差公式进行重新定义，将其中的样本算术平均值替换为 我们的期望值 【1】。 我代表月亮 重新给它命名为：“一差公式”！ 公式如下：
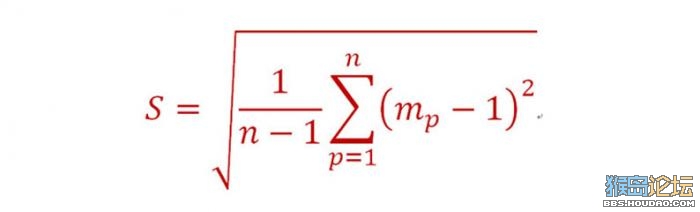
计算极其复杂，数据量庞大，过程就不提了，计算结果如下：
企太郎 “一差”= 2.725
酷企鹅 “一差”= 2.635
茶杯犬 “一差”= 2.536
童话驯鹿“一差”= 1.989
蓝晶龙 “一差”= 1.77
注：“一差”越小，离散度越小，稳定性越好
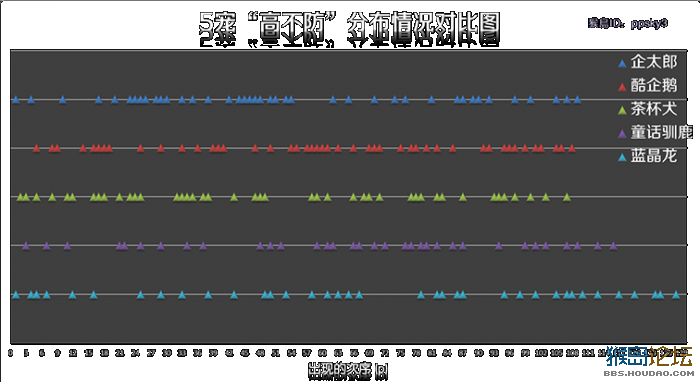
X轴方向： 从各宠物的散点图中可以看出，所有宠物的N不防算术平均值都是大于2小于3的数。那么为了简化计算，我将1不防和2不防归为一类，视它们的值相同，称它们为“低不防”； 将3不防及以上 归为一类，视它们的值相同，为“高值”，称它们为“高不防”。 我问大家：如果“低不防”分布均匀，“高不防”是不是也应该是分布均匀？反之亦然。即计算“低不防”的均匀系数等效于计算“高不防”的均匀系数。 因为“低不防” 的样本太多，计算量庞大，所以我选择计算“高不防”的均匀系数！ 5只宠物“高不防”在时间轴上的分布情况如下图：
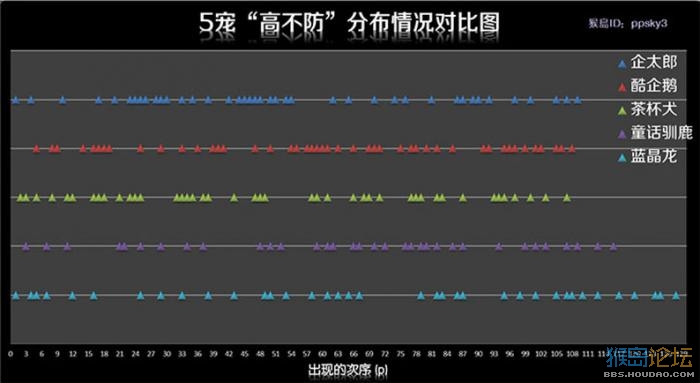
X轴表示 “高不防”出现的次序（即每个高不防的座位），Y轴表示 5只宠物。我要研究的是这5只宠物高不防的分布均匀系数。
我借用 美国农业工程师 J. E. Christiansen 提出的均匀系数公式，并重新定义它的物理意义：
计算结果为：
企太郎的均匀度= 52
酷企鹅的均匀度= 56
茶杯犬的均匀度= 45
童话驯鹿的均匀度= 59
蓝晶龙的均匀度= 51
注： 均匀度越高，越稳定。
由于“一差”和“均匀度”的计算结果 等级相差较大，而“一差”和“均匀度”对宠物防御稳定性的影响是平等的，所以我把“一差”的计算结果转换为与“均匀度”相同的数值等级，转换方法为： “一差”的平方的10倍， 又考虑到一差是越低越好，而均匀度是越高越好，所以综合两方面的因素时，我将“一差”方面的数值倒过来，即用100减去（“一差”的平方的10倍）来表示Y轴方向的稳定数值。这个数值计算结果如下：
企太郎 Y轴影响值= 26
酷企鹅 Y轴影响值= 31
茶杯犬 Y轴影响值= 36
童话驯鹿Y轴影响值= 61
蓝晶龙 Y轴影响值= 69
最终稳定系数为上述二值的平均值：【 即 （均匀度+Y轴影响值）/2 】
企太郎的稳定系数= 39
酷企鹅的稳定系数= 43.5
茶杯犬的稳定系数= 40.5
童话驯鹿稳定系数= 60
蓝晶龙的稳定系数= 60
注：稳定系数越高，宠物防御越稳定！
性格分析：
这个就直接上图吧，过程略
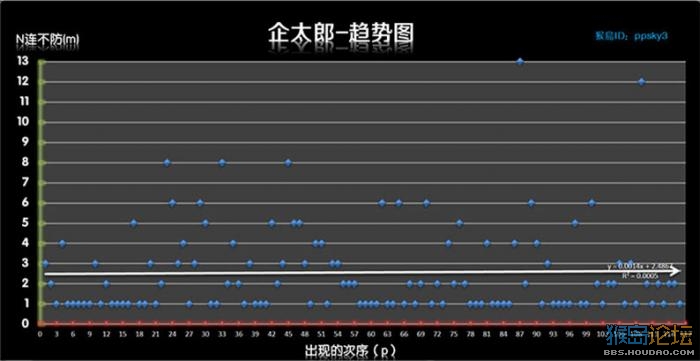
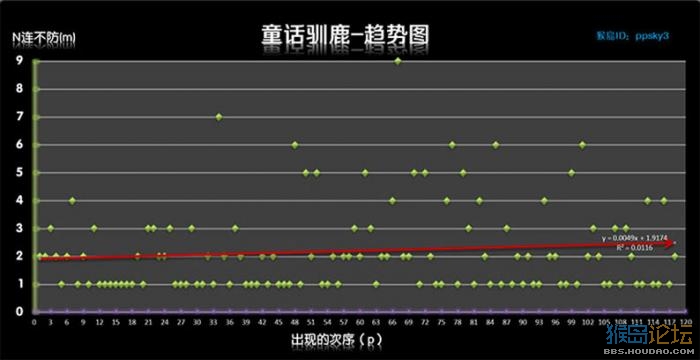
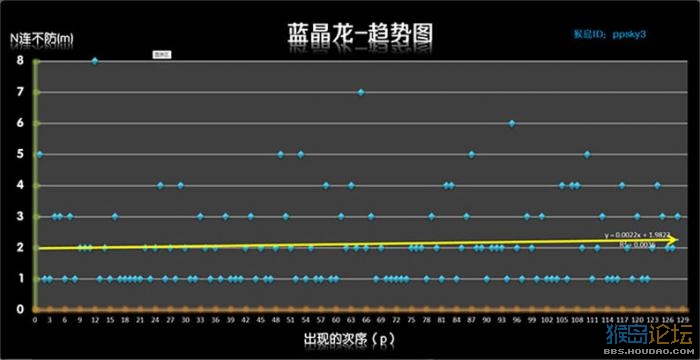
图中带箭头的趋势线表示的是“不防御”的趋势， 其中茶杯犬 走势向下，说明它的防御性能会随着时间的流逝变得优秀，我把它的性格定义为“愈战愈勇”；其它4个都是走势向上，防御性能会越来越弱，性格应定义为“愈战愈挫”。但是其中企太郎和蓝晶龙 走势较为平缓，也可以定义为“保守型”
结论汇总：
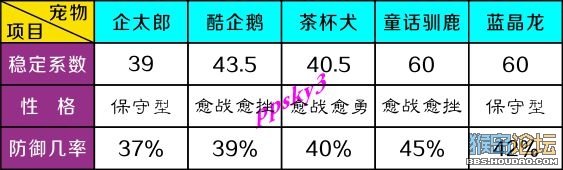
附件：
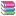原始数据扫描件.zip[点击下载](495 K) 下载次数:3 累计下载获得 ＤＢ 6 刀查毒链接：http://r.virscan.org/report/b2f7564d4edfe240624333b981cacde9.html
[ 此帖被ppsky3在2013-07-06 22:56重新编辑 ]
牛了一笔
